Программная система удаленного решения однородных линейных диофантовых уравнений в неотрицательных целых числах
Традиционно исследование диофантовых уравнений проводилось в теории чисел и дискретном анализе. Потребности приложений стимулировали развитие теорий целочисленных полиэдров и вполне двойственной целочисленности, опирающихся на введённое F. Giles и W. Pulleyblank понятие базиса Гильберта (БГ) [1]. Растёт число прикладных исследований, в которых в качестве математического аппарата применяются системы однородных линейных диофантовых уравнений с целочисленными коэффициентами и решениями в неотрицательных целых числах (одНЛДУ). Конечный и единственный БГ (не основан на понятии линейной зависимости) содержит все “неразложимые” решения, что позволяет описать множество решений системы.
Дискретные модели на основе систем одНЛДУ и их БГ (линейные диофантовы модели) применяются в различных областях, например, задача ассоциативно-коммутативной унификации [2], построение универсального тестового множества для семейства целочисленных линейных оптимизационных задач [1], параллельный доступ к кэшпамяти и массивам [3], модели маршрутов в сетях ЭВМ [4].
Практическое использование линейных диофантовых моделей требует эффективных алгоритмов нахождения БГ (НБГ) и их протестированных реализаций, но в этой области существует серьезный пробел. Известен ряд алгоритмов НБГ на основе различных математических методов: верхние границы компонент базисных решений [5], покомпонентное построение решений, начиная с нулевого [6], преобразования производящих функций [7], нахождение базисных решений с минимальным носителем и последующим построением оставшихся базисных решений как рациональных положительных комбинаций [8, 9], нахождение базиса Гребнера идеала в кольце полиномов [5] и др. Эти алгоритмы представлены без верхних оценок сложности, их реализация не проверена массовым тестированием, и они применимы на практике лишь для малых размерностей (до 15..20 переменных и уравнений).
Задача НБГ является вычислительно трудоёмкой, поскольку число базисных решений может экспоненциально зависеть от размерности системы и абсолютных величин её коэффициентов (нижняя оценка сложности) [1]. Следовательно, актуальными являются исследования частных классов диофантовых систем, для которых могут быть получены эффективные алгоритмы НБГ. При этом эффективным будем считать алгоритм, сложность которого ограничена полиномиально от числа уравнений, неизвестных и базисных решений (псевдополиномиальный алгоритм). В [10−12] получен один из таких частных классов — ассоциированные с контекстно-свободными (КС) грамматиками диофантовы системы (системы одАНЛДУ).
В статье представлена программная система (ПС) Web-SynDic, разрабатываемая на кафедре информатики и математического обеспечения Петрозаводского государственного университета с 2003 года. ПС реализует через web-обозреватель доступ к двум авторским псевдополиномальным алгоритмам НБГ для систем одАНЛДУ: Syntactic [10, 11] и TransSol [12], а также к алгоритмам SlopesSys [9]), lp_solve (http://lpsolve.sourceforge. net/) и GLPK (http://www.gnu.org/software/glpk/). ПС обеспечивает также массовое тестирование реализаций алгоритмов НБГ и их экспериментальное исследование [13].
Однородные линейные диофантовы уравнения, ассоциированные с КС-грамматиками
Обозначим множества целых и неотрицательных целых чисел как Z и Z+ . Однородной системой неотрицательных линейных диофантовых уравнений (система одНЛДУ) называется (0 — нулевой вектор):
Ax = 0, A Zn🞩m, x
Zm (1)
с n уравнениями, m неизвестными, целочислен- ными коэффициентами и неотрицательными целыми решениями.
Ненулевое решение системы (1) называется неразложимым, если оно не может быть пред- ставлено как сумма двух ненулевых решений этой же системы. Базисом Гильберта (БГ) назы- вается множество всех неразложимых решений H = {h(1), h(2),..., h(q)} которое конечно, единственно и определяет общее решение системы (1) как [1]
Перенося в каждом уравнении из (1) члены с отрицательными коэффициентами в другую часть уравнения, получаем представление A'x = A''x. С алгебраической точки зрения рассматриваемый нами класс ассоциированных с КС-грамматиками диофантовых систем получается ограничением на матрицу A' следующим образом.
Возьмём разбиение m-отрезка натурального ряда: ,
, Ik попарно не пересекаются и не пусты, 0 < n ≤ m. Пусть E = E(I) {0,1}n🞩m, где E = 1 <=> i I . Тогда система одАНЛДУ есть Ex = Ax для A ≥ 0 , или
Следуя [10] рассмотрим, как по КС-грам- матике без терминальных символов построить (3). Случай произвольной формальной граммати- ки исследован в [11].
Пусть грамматика состоит из m правил и n нетерминальных символов
. Терми- нальный алфавит пуст. Правила грамматики имеют вид ri = (Nk → αi) для i = 1,2,..., m, некоторого k
{1,2,..., n} и некоторой цепочки αi из нетерминалов (возможно, пустой). Тогда определим Ik как множество индексов тех правил грамматики, левая часть которых равна N , а α = |α | , где |αi|Nk ≥ 0 есть число вхождений Nk в αi. Таким об- разом, неизвестные системы (3) ассоциируются с правилами грамматики, а уравнения − с нетерми- налами. Значение xi определяет число применений правила ri в некотором грамматическом выводе.
Существует соответствие между множеством всех решений системы (3) и множеством всех циклических выводов {N * N } в грамматике, определяемое следующей теоремой [10]. Здесь под простым циклом понимается циклический вывод Nk
* Nk, не содержащий в себе другого циклического вывода.
Теорема 1 [Общий вид решения системы одАНЛДУ]. Вектор x Zmявляется решением (3) тогда и только тогда, когда определяется чис- лом применений правил в конечном множестве циклов {N
* N }. Решение является базисным (x
H) тогда и только тогда, когда x соответствует в точности одному простому циклу.
В [12] получено алгебраическое преобра- зование произвольной системы одАНЛДУ, по- зволяющее применять для задачи НБГ метод исключения неизвестных и уравнений. Назовём уравнение k в (3) разрешённым относительно L-неизвестных, если его можно представить в виде где L ≠ Æ есть множество индексов неизвестных, которые не встречаются в оставшихся уравнениях. Пусть S(1) − исходная система, k = 1.
- Выбираем в S(k) уравнение, которое можно разрешить для L = Lk ≠ Æ. Если такого уравнения нет, то преобразование завершено. Без потери общности считаем, что выбрано первое уравнение.
- S(k) представим в виде
(4)
- S(k+1) является системой одАНЛДУ, содержит на одно уравнение и |L | неизвестных меньше. Полагаем k := k + 1 и переходим на шаг 1.
Через r итераций получаем трапециевидную форму:
(5)
При этом система (3), как показано в следующей теореме, сводится к одному из двух простых классов.
Теорема 2 [Сведение системы одАНЛДУ].
Система S(r) равносильна либо системе одАНЛДУ с одним уравнением (при r = n)
для некоторого I' Ì {1,2...,m}, (6) либо симметричной системе одАНЛДУ (при r < n)
(7)
для разбиений I' = {I ,...I ,Z,F} и J' = {J ,...J ,Z,F} отрезка {1,2,...,m}.
Алгоритмы
В ПС Web-SynDic подключены два авторских алгоритма НБГ − Syntactic [11] и TransSol [12] −и алгоритм SlopesSys [9]. Последний является универсальным, позволяя решать задачу НБГ для систем одНЛДУ. Также используются алгорит- мы поиска частного решения на основе методов
целочисленного линейного программирования: пакеты LP_solve и GLPK. Для автоматического построения тестовых и эталонных диофантовых систем подключены авторские алгоритмы генерации [14]: JourdanGen, GaussGen, и ExtGaussGen. Авторские алгоритмы имеют псевдополино-
миальную сложность (табл. 1) и реализованы на языке ANSI C (табл. 2). Верхние оценки сложности получены в модели вычислений с произ- вольным доступом к памяти (RAM). Сложность оценивается как функция от трёх параметров: 0 < n < m − число уравнений и неизвестных, Q − максимальный размер БГ промежуточных систем (зависит от алгоритма). В ряде случаев вместо Q возможно использовать q (размер БГ исходной системы)
Алгоритм Syntactic. Задача НБГ для (3) сво- дится к синтаксическому разбору на основе тео- ремы 1. Построение грамматических выводов для базисных решений использует подвыводы (ком- позиция выводов), соответствующие базисным решениям ряда “близких” систем, т. е. одновре- менно решается семейство систем. Параметр Q ограничивает максимальный размер БГ для этого семейства. Композиция выводов использует идеи алгоритмов поиска кратчайших путей в орграфе для перечисления базисных решений. Так, моди- фикация алгоритма Дейкстры позволяет перечис- лить простые выводы Nk + ε, которые определя- ют БГ системы Ex = Ax + ek, где ε − пустая цепочка, ek − стандартный единичный вектор. Далее строятся простые выводы Nk
+ Nl, определяющие БГ системы Ex + e = Ax + e , как N
+ αN β
+ N . В альтернативном варианте простой вывод Nk
+ Nl получается из Nk
+ l
+ ε. В случае k = l на- ходим БГ (3). Отбор неразложимых решений ис- пользует ряд критериев и достаточных условий.
Алгоритм TransSol. Задача НБГ для (3) сво- дится к задаче НБГ для простых классов (6) или (7) на основе теоремы 2. В случае (6) НБГ сво- дится к последовательному решению уравнений Фробениуса с единичными коэффициентами: åiÎI xi = a j для каждого j I. Система (7) определяет циркуляцию потока в некотором орграфе, сводя задачу НБГ к поиску простых контуров.
Таблица 1
Оценки сложности авторских алгоритмов НБГ и генерации
БГ исходной системы вычисляется подстанов- кой базиса: выполняются шаги преобразования к трапециевидной форме в обратном порядке. При этом задача НБГ для очередной системы S(k) сво- дится к уравнению вида (6), а Q ограничивает раз- мер его базиса для всех k = 1,2,..., r – 1. На каждом шаге прямым перебором исключаются разложи- мые решения. Однако в [14] получены классы си- стем одАНЛДУ, где такой отсев не требуется.
Алгоритм SlopesSys. Универсальный алго- ритм НБГ для (1). Находятся базисные решения с минимальным носителем [8]. Оставшиеся реше- ния ищутся перебором по решётке граней конуса вещественных неотрицательных решений систе- мы (с отсевом нецелочисленных и разложимых решений). В промежуточных подсистемах вы- деляются три неизвестных и применяется алго- ритм НБГ для уравнения с тремя неизвестными. Значения оставшихся неизвестных определяются перебором в рамках известных верхних границ. Переборный характер приводит к трудоёмким вычислениям, и практическое использование алгоритма возможно только для малых систем (n, m ≤ 20, max|a | ≤ 100). Алгоритм сопоставим по экспериментальной трудоёмкости с известны- ми универсальными алгоритмами [5−8].
Алгоритмы поиска частного решения. Ис- пользуют свободно распространяемые оптимиза- ционные пакеты lp_solve и GLPK. В отличие от алгоритмов НБГ они выполняют поиск частного ненулевого решения (3), используя следующую задачу ЦЛП:
(7)
Последнее ограничение отсекает нулевое реше- ние. Алгоритмы используются при тестировании алгоритмов НБГ: выполняется проверка разложи- мости частного решения (8) по найденному БГ.
Алгоритмы генерации. Строят диофантовы системы (3) вместе с их БГ при заданных ограни- чениях. Входные параметры: число уравнений и неизвестных (n, m), ограничения сверху на коэф- фициенты (aki ≤ a) и БГ (hi ≤ h, q ≤ q). Результат: E(I), A, H. Алгоритмы основаны на теореме 2, начиная построение с простой системы (6) или (7). Как и в алгоритме TransSol, выполняется обратное преобразование с подстановкой БГ до получения требуемой системы и её БГ. Алгоритм JordanGen использует идею диагональной формы матрицы в преобразовании Жордано−Гаусса, строя систему с БГ из q = m – n стандартных единичных векто- ров. Алгоритм GaussGen использует идею треу- гольной формы матрицы в методе Гаусса, строя систему с q = m – n и (0,1)-значениями в базисных решениях. Алгоритм ExtGaussGen расширяет предыдущий: нет зависимости q от n и m, а значе- ния базисных решений − произвольные.
Таблица 2
Сводные характеристики реализации
Программная система
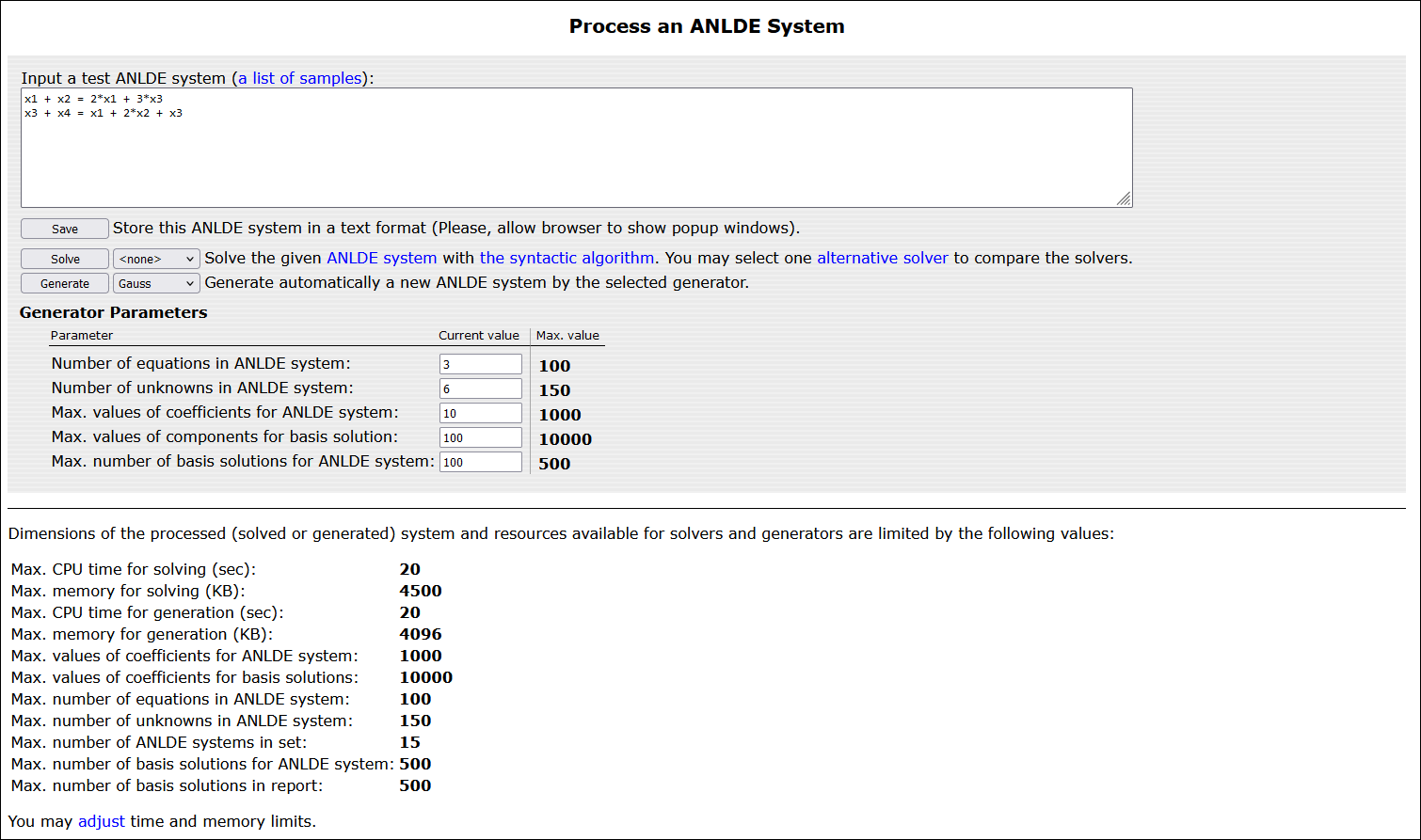
ПС Web-SynDic (http://websyndic.cs.karelia.ru/) предназначена для удалённой работы с реализа- циями алгоритмов решения диофантовых уравне- ний и предоставляет два основных сервиса [13].
Сервис решения диофантовых систем включает, во-первых, тестирование, эксперимен- тальное исследование и сравнительный анализ программных реализаций алгоритмов решения. Во-вторых, сервис позволяет решать задачу НБГ, в том числе и для диофантовых систем большой размерности. Сервис генерации диофантовых си- стем предназначен для автоматического построе- ния систем с заданными свойствами. При тести- ровании алгоритмов НБГ генерируются тестовые системы с известным БГ для проверки решений, получаемых тестируемым алгоритмом. При экс- периментальном исследовании генерируются эталонные системы, позволяющие статистически охарактеризовать и сравнить трудоёмкость (временную и ёмкостную) исследуемых алгоритмов на заданном классе входных данных.
Рис. 1. Высокоуровневая архитектура ПС Web-SynDic
Рис. 2. Диаграмма классов подсистемы Algorithm server
Высокоуровневая архитектура ПС пред- ставлена на рис. 1. Клиентом выступает web- обозреватель. Работа пользователей происходит в режиме сессий. Запросы поступают в подсисте- му Web-server, которая переводит данные во вну- тренний формат и передает их подсистеме Session processing, обеспечивающей связь с остальными подсистемами. Подсистема Activity statistics на- капливает статистику использования и формирует отчеты. Для измерения потребляемых ресурсов используется авторская ПС alg_analyzer. Подси- стема Management управляет настройками и огра- ничениями пользователей. Подсистемы Activity statistics и Management работают с хранилищем данных Data store, где хранится информация о зарегистрированных пользователях.
Подсистема Algorithm server является ключевой с точки зрения обработки запросов (рис. 2). Она реализует объекты и операции предметной области, обеспечивает взаимодействие с алгоритмами решения и генерации диофантовых систем. Все эти алгоритмы представлены в ПС только исполняемыми модулями, что защищает их ис- ходный код от несанкционированного доступа.
Пользователь инициирует запрос, который разбивается на базовые задачи (каждая из них требует однократного вызова внешнего алго- ритма, реализуется в виде объекта класса Task). Поддерживаются задачи решения (класс SolTask) и генерации (класс GenTask). Каждая задача хра- нит объект класса ANLDE (диофантова система, набор диофантовых систем или запрос на гене- рацию) и информацию о нахождении задачи в одной из двух очередей обработки базовых задач (объект Solver Spooler для задач решения и объ- ект Generator Spooler для задач генерации). Далее этот объект полностью отражает состояние обра- ботки запроса.
Очереди обработки задач работают параллельно. Очередная задача передается объекту класса Module для взаимодействия с внешними алгоритмами. Интерфейс реализуется потомка- ми класса Module: классы Solver и Generator. Для подключения внешнего алгоритма создается спе- циализированный потомок одного из этих двух классов.
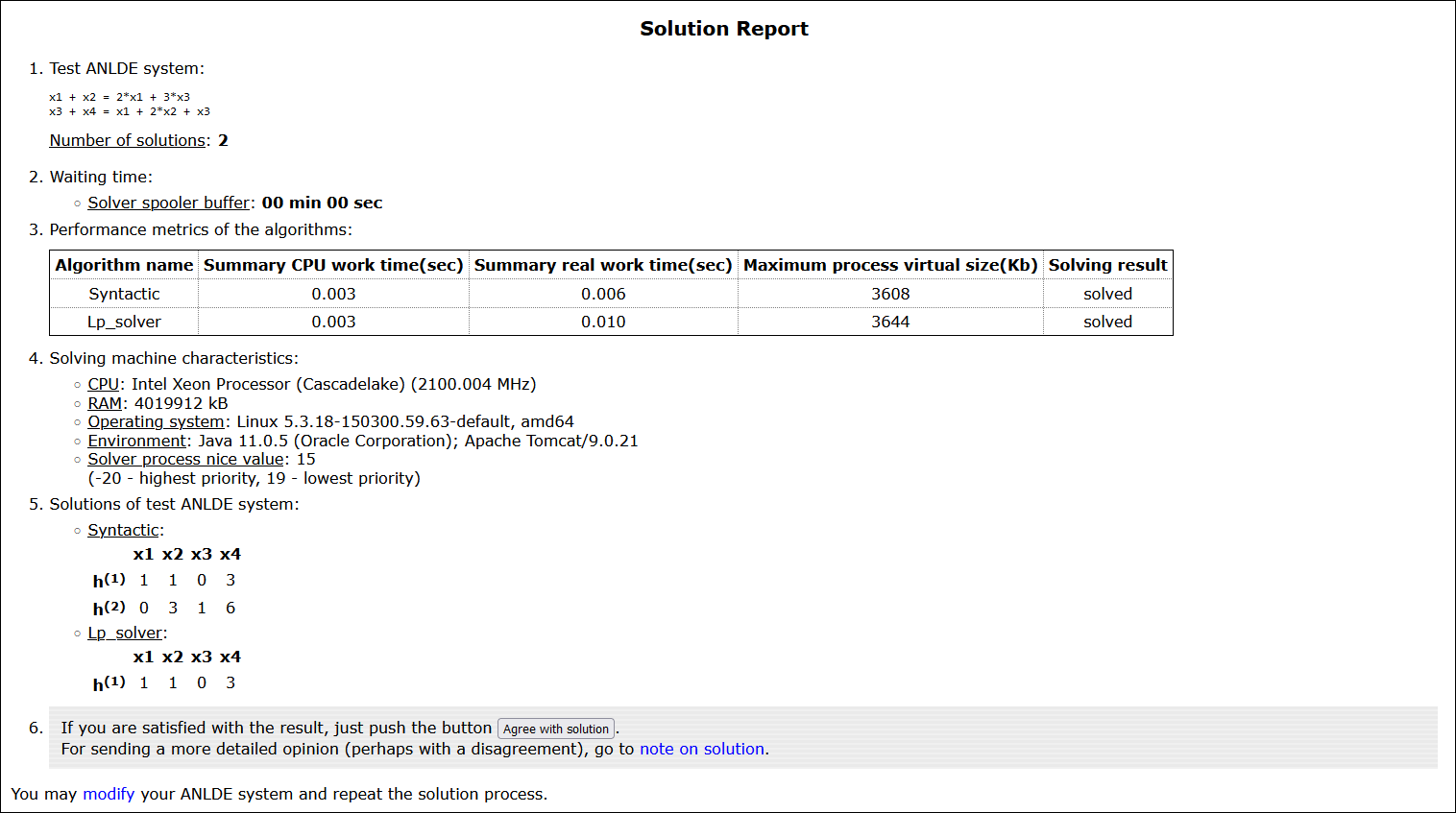
Результат внешнего алгоритма сохраняется в объекте класса Solver Outcome, включая харак- теристики диофантовой системы или их набо- ра (класс ANLDECh), решения (БГ или частное, класс Solutions), характеристики ЭВМ (класс Server), результат проверки решений (класс Check Solutions) и метрики трудоёмкости (класс Solver Metrics). Объект класса Solver Process хранит характеристики алгоритма решения. После решения всех базовых задач запроса подсистема Session processing формирует отчет (рис. 3).
Идентификация пользователей использу- ет входное имя и пароль. Зарегистрированным пользователям доступна обратная связь, персо- нальные настройки и управление такими параме- трами, как допустимые время решения и объём памяти, границы коэффициентов диофантовых систем, допустимый размер БГ и др. Для ано- нимных пользователей настройки сохраняются только на время работы сессии. Зарегистриро- ванный пользователь может получить статус привилегированного, у которого отсутствуют ограничения на максимальные значения пара- метров решения и генерации, что позволяет ре- шать системы больших размеров. Администра- тор управляет работой системы и имеет доступ к статистике её использования.
ПС Web-SynDic реализована на платформе Java (Java SDK 1.6.0), (табл. 2). Интерфейс поль- зователя − англоязычный. Текущая версия ПС ра- ботает под управлением сервера Apache Tomcat (5.0, JRE 1.6.0).
Рис. 3. Пример отчёта о решении
Таблица 3
Части экспериментального исследования
Тестирование и эксперименты
В экспериментальном исследовании прово- дились как массовое тестирование реализаций авторских алгоритмов НБГ и генерации, так и сравнительный анализ их трудоёмкости. Отме- тим, что в ПС WebSynDic любой запуск алгорит- ма является тестом.
Исследование включает три части, каждая состоит из серий (табл. 3). Серия использует на- боры диофантовых систем, каждый из которых построен некоторым генератором при заданных ограничениях. Для коэффициентов в (3) исполь- зуется норма ||A|| = max a.
Часть I. Выполнялось массовое тестирование алгоритма Syntactic, который является первым ав- торским алгоритмом НБГ для систем одАНЛДУ. Тестирование его реализации было исходной зада- чей при разработке ПС Web-SynDic. Использова- лись разнообразные наборы тестовых диофантовых систем, в том числе и учитывающие внутренние особенности алгоритма (табл. 3, серии I.1 и I.2). Допустимое время на решение одной системы со- ставляло от 6 ч до 3-х суток в сериях I.1-3 и 100 с в серии I.4. Небольшое число тестовых систем в серии I.3 вызвано временными затратами пакета lp_solve для тестовой задачи ЦЛП (вплоть до ис- ключения ряда тестовых систем из-за превышения допустимого времени). В то же время, алгоритм Syntactic находил корректное решение каждой из тестовых систем в течение нескольких минут.
Часть II. Выполнялось сравнение с универ- сальными алгоритмами. Исследовались три алго- ритма НБГ: Syntactic и TransSol − специализиро- ванные для (3) и SlopesSys − универсальный для (1). Последний не позволяет решать диофантовы системы за приемлемое время уже для средних размеров (m > 15...20), а для наборов малых систем (m ≤ 15...20) отбирались только те системы (не учи- тываются в табл. 3 и 4), которые удалось решить за отведённое время (10 мин в сериях II.1 и II.2, 100 с в серии II.3). Алгоритмы Syntactic и TransSol допу- скают корректное решение всех сгенерированных систем малых и средних размеров за отведённое время. В табл. 4 для серий II.1 и II.2 представ- лены сравнительные измерения затраченного системного времени (процессор, в с) в виде выборочных медиан, каждая вычислена на основе двадцати эталонных систем.
Таблица 4
Системное время (с) работы алгоритмов НБГ в зависимости от числа неизвестных m (Intel Xeon 2.80 ГГц, ОЗУ 1 Гб, Linux 2.6.27)
Часть III. Для различных классов эталонных диофантовых систем выполнялось сравне- ние алгоритмов Syntactic и TransSol (табл. 3). В сериях III.1-5 алгоритмы JordanGen, GaussGen и ExtGaussGen генерировали наборы по 5000 си- стем каждый. В серии III.6 использовался только алгоритм ExtGaussGen. Исследовались влияние размеров входных и выходных данных (n, m, ||A||, q). Допустимое время решения одной системы равнялось 5 мин. При его превышении или из-за внутренних ограничений реализации хотя бы для одного из алгоритмов эталонная система игно- рировалась при подсчёте сравнительных оценок. Пример полученных экспериментальных зависи- мостей представлен на рис. 4.
Эксперименты части III показывают, что алгоритм TransSol эффективнее, чем алгоритм Syntactic: потребление памяти и общее время мень- ше на 10–35 % и до двух раз, соответственно. Для алгоритма Syntactic получены системы (до 25 %), которые не удалось решить. Они характерны для алгоритма генерации ExtGaussGen при больших значениях q. Для алгоритма TransSol такое не на- блюдается: решены все предложенные системы. Отметим, что алгоритм TransSol и используемые алгоритмы генерации основаны на одном методе (теорема 2), т. е. успешно сгенерированная систе- ма допускает эффективное решение. В частности, для таких систем не требуется трудоёмкая операция отбора неразложимых решений в алгоритме TransSol.
В целом результаты экспериментального ис- следования подтверждают пригодность специ- ализированных алгоритмов Syntactic и TransSol для практического использования и позволяют говорить о высоком качестве программных реа- лизаций этих алгоритмов.
Представленная в статье ПС WebSynDic реа- лизует доступ через web-обозреватель к алгорит- мам НБГ линейных диофантовых систем, а также к соответствующим средствам тестирования и экспериментального исследования на основе ав- томатической генерации систем с известным БГ.
Два авторских алгоритма НБГ работают с дио- фантовыми системами, ассоциированными с КС- грамматиками. Объемные численные эксперимен- ты показывают, что эти алгоритмы пригодны для решения прикладных задач, т. к. они существенно эффективнее, в том числе для больших систем, чем известные универсальные алгоритмы.
ПС является удобным инструментом для улучшения существующих и экспериментально- го исследования новых алгоритмов НБГ, что яв- ляется одним из направлений наших дальнейших работ. Также предполагается дополнять ПС диа- логовыми компонентами в терминах предметных областей для решения соответствующих прикладных задач.
а) б)
Рис. 4 Зависимость общего времени НБГ (с) от размера БГ, серия III.5, набор по алгоритму ExtGaussGen
(Intel Xeon 2.50 ГГц, ОЗУ 2 Гб, ОС Linux Suse 10.2 gcc 4.1.2). Указаны выборочное среднее и процентили (а) алгоритм Syntactic, (б) алгоритм TransSol. Выбор. среднее (-); Q (5 %) (--); Q (50 %) (-- -- --); Q (95 %) (- - - - - -).
Авторы выражают свою благодарность К. А. Кулакову и М. А. Крышеню, которые внесли существенный вклад в реа- лизацию ПС Web-SynDic и продолжают ее сопровождение.
Пример использования системы